Forum modelarskie RC , projektowanie CAD

Na razie nie mam weny aby ciągnąć Hortena, postanowiłem napisać taki wątek.

Może się komuś przyda, a przy okazji przedstawię program OpenVSP http://openvsp.org/download.php
Jest to program typu opens ource stworzony przez NASA.
Program ten jest rekomendowany przez FAA (amerykański nadzór lotniczy) do projektowania ultralekkich samolotów.

Na razie wykorzystuję kilka modułów, ale aerodynamikę i mechanikę lotu robię w XFLR5 lub Flow5. Moim zdaniem lepiej się spisują.

OK zaczynamy projektowanie śmigła dla wybranego silnika do naszego modelu.
Ktoś mi powie - przecież jest eCalc Prop - to bull sh....

Generalna zasada jest taka, że moc użyteczna na wale silnika lub przekładni musi być równa momentowi oporowego śmigła.

A. Projektowanie śmigła - co nam potrzebne?

1) Moc użyteczna silnika = Pus, jest to moc max pomnożona przez sprawność silnika
Wybrany silnik elektryczny, np. AXI 5345/16

Pmax = 4200 W
sprawność >85% dla dość dużego zakresu prądowego, przyjmujemy =85% =0,85

Pus = 4200 * 0,85 = 3750 W

2) maksymalne obroty na wale silnika, lub przekładni
nasz swlnik ma kV = 195
będziemy go zasilać akumulatorem 10S U = 37 V
n = kV * U = 195 * 37 = 7215 obr/min = ~ 120 obr/s = 755 rad/s

3) maksymalna prędkość naszego modelu w locie poziomym
zakładamy Vmax = 130 km/h =~ 36 m/s

Ms = Pus/n = 3750/755 = 4,73 Nm

Teraz musimy obliczyć/dobrać takie śmigło aby jego moment oporowy był równy obliczonemu momentowi silnika Ms = 4,73 Nm

Aby obliczyć śmigło potrzeba jest określić typ śmigła i pozyskać jego charakterystyki

W Polsce bardzo popularny jest: "Katalog śmigieł" prof. inż. Bukowskiego.

Jest też dostępny NACA REPORT 640 z podobnymi charakterystykami śmigieł - załączyłem

Wracając do "Katalogu śmigieł" prof. inż. Bukowskiego.
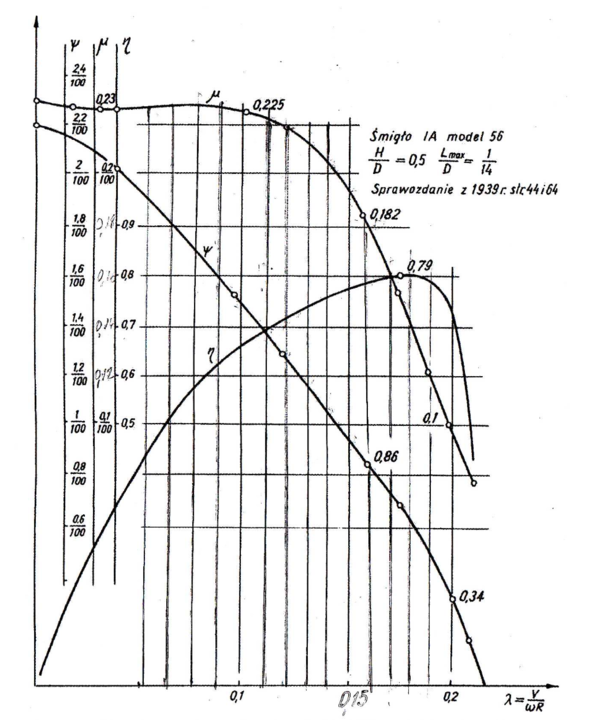
Weźmy poniższą charakterystykę


Jest to charakterystyka śmigła typu IA, model M56
Omówimy ten wykres - to podstawowy wykres przy projektowaniu śmigieł. Każdy typ śmigła ma taki wykres.

Jakie dodatkowe informacje możemy wyczytać z wykresu:
H/D - czyli stosunek skoku do średnicy śmigła = 0,5. tak naprawdę H/D może być w zakresie:

0,45 <= H/D <= 0,55

Lmax/D = 1/14
szerokość łopaty do średnicy, może być w zakresie pomiędzy 1/12 a 1/15

λ - posuw, często oznaczany przez: J

Jest jednak różnica pomiędzy λ a J, szczególnie jeśli korzystamy z anglojęzycznych publikacji i jednostki nie są w układzie SI.

λ = V/(ω*R)
V - maksymalna prędkość lotu poziomego w [m/s]
ω - prędkość obrotowa w [rad/s]
R - promień śmigła w [m]


J = V(n*D)
V - maksymalna prędkość lotu poziomego w [m/s]
n - prędkość obrotowa w [obr/s]
D - średnica śmigła w [m]

W każdym przypadku musimy korzystać z właściwych wykresów i wzorów.

Co jeszcze jest na wykresie?

μ - cecha mocy śmigła, tak naprawdę wg powyższego wykresu μ/100 (bezwymiarowe)
ψ - cecha ciągu śmigła, tak naprawdę wg powyższego wykresu ψ/100 (bezwymiarowe)
η - sprawność śmigła, (bezwymiarowe)


Wracamy do obliczania śmigła.

Tak naprawdę obliczając śmigło poszukujemy jego średnicy, aby moment oporowy śmigła był równy obliczonemu momentowi silnika.

Jaki jest zatem wzór na moment oporowy śmigła?
Wg. "Katalogu śmigieł" prof. inż. Bukowskiego.

Mos = 0,5*ρ*μ*π*ω^2*R^5 [Nm]
ρ - gęstość powietrza = 1,225 (pomijam jednostki)
μ - cecha mocy śmigła, tak naprawdę wg powyższego wykresu μ/100
ω - prędkość obrotowa w [rad/s]
R - promień śmigła w [m]


Podstawiając do wzoru wartości za π i ρ mamy wzór.

Mos = 1,92*μ*ω^2*R^5,


B. Obliczamy/poszukujemy średnicy - jak to zrobić?

Np.: makietowa średnica śmigła wychodzi nam 550 mm = 0,55 m
Promień - R = 0,275 m

Poszukujemy zatem średnicy jak najbliższej temu wymiarowi, aby spełnić warunek równowagi momentów
Aby cokolwiek znaleźć na wykresie musimy znać posuw śmigła - λ (pozostajemy w układzie SI)

λ = V/(ω*R)


mamy dane:
Ms = 4,73 [Nm]
Vmax = 36 [m/s]
ω = 755 [rad/s]
promień śmigła makietowego R = 0,275 [m]

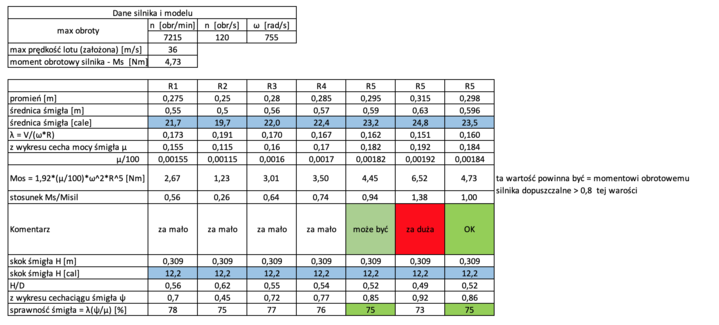
Szukamy średnicy i obliczamy moment - najlepiej w tabelce
Tabelkę robimy w arkuszu Excel tak aby od razu wykonywać obliczenia.

Poniżej zrzut z arkusza - wstawię arkusz z formułami, ale trochę później, muszę go dopracować (uporządkować, dodać komentarze)


Mamy dobraną średnicę - tak naprawdę dwie średnice spełniają nasze wymagania.
Sprawdzamy czy śmigło o takiej średnicy może być zainstalowana - wychodzi nam o 40 lub 46 mm większa od makietowej.

Co zrobić gdy jest za duża? Założyć mniejszą prędkość maksymalną modelu w locie poziomym.
Załóżmy, że średnica śmigła 0,596 jest OK.

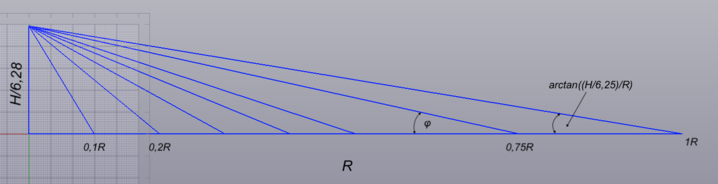
C. Geometria śmigła - wyznaczenie kąta beta łopaty w 0,75R śmigła.

Rysujemy trójkąt prostokątny o wymiarach przyprostokątnych: R i H/6,28
Skąd te 6,28?
Tu już dokonałem uproszczenia. bez uproszczeń trójkąt ten ma przyprostokątne o długości: H i 2π R
2π = 6,28


φ - kąt skoku łopaty w 0,75R - dla tego kąta określimy kąt beta dla łopaty śmigła

Zaznaczyłem kilka położeń %R
W pozycji 0,75R będziemy wyznaczać kąt beta łopaty
Dawniej rysowało się ręcznie wg tego co np. zamieścił Pan Wiesław Schier w jednej ze swoich książek.
Teraz przy pomocy np. OpenVSP potrzebne nam:
0,1R lub 0,2R, 0,75R, oraz 1R


rysowanie śmigła wg "Miniaturowe lotnictwo" Wiesława Schiera

C.1 Ruch obrotowy śmigła - niuanse

Rozważmy ruch przekroju łopaty w 0,75R (ruch profilu łopaty w tej sekcji)




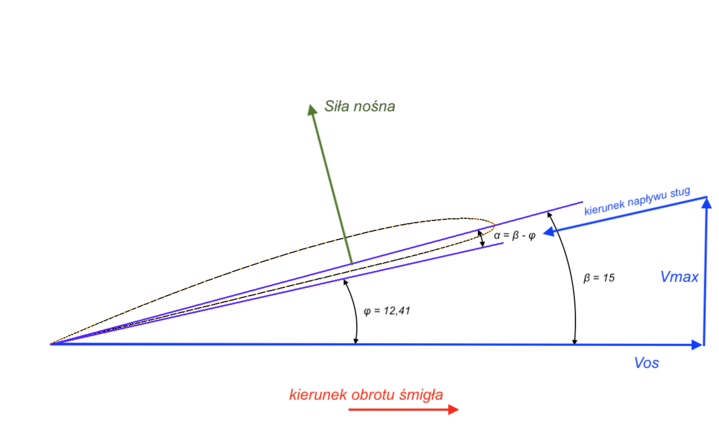
Zaznaczone:

Vmax - jest to maksymalna prędkość jaką powinien uzyskać model z tym śmigłem (na taką liczyliśmy śmigło)
Vos - prędkość obwodowa końcówki łopaty śmigła Vos = ω * R (przy maksymalnych obrotach silnika,) Rozpatrujemy przekrój łopaty w 0,75R.
kąt fi = 12,41 st - tyle otrzymaliśmy z obliczenia śmigła średnica x skok
kąt beta - zaleca się używać znormalizowanych kątów: 15, 20, ...

Przyjmując kąt beta = 15 stopni, otrzymujemy kąt natarcia łopaty w tym przekroju = 15 - 12,41 = 2,59 stopnia. Jest to kąt pomiędzy kierunkiem napływu strug na profil łopaty śmigła (w j. angielskim zwany: Relative flow) a cięciwą profilu.

Zaznaczyłem kierunek siły nośnej łopaty w tym przekroju (zawsze prostopadły do kierunku napływu strug)
To jest przypadek lotu poziomego z maksymalną prędkością.

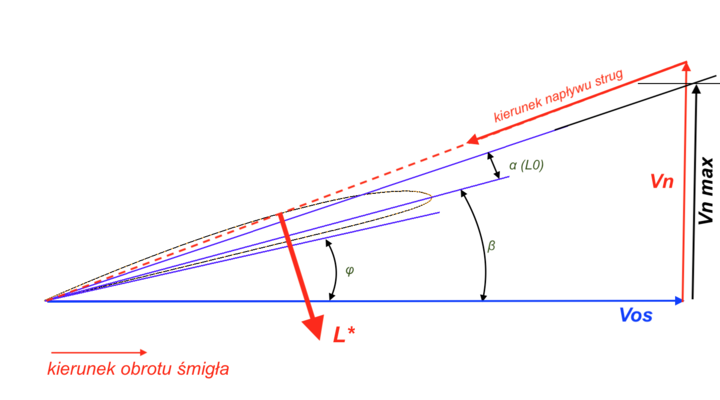
Teraz zajmijmy się maksymalną nieprzekraczalną prędkością nurkowania.

Właśnie podczas nurkowania możemy przekroczyć maksymalną dozwoloną prędkość lotu dla śmigła.

Popatrzmy na ten rysunek


Na rysunku widać, że podczas nurkowania osiągnęliśmy prędkość Vn dla której to oraz dla maksymalnych obrotów silnika, kierunek napływu strug na profil śmigła jest taki jak zaznaczono. Jego kąt jest większy od sumy kątów β + α (L0)

Co to jest α (L0) ?
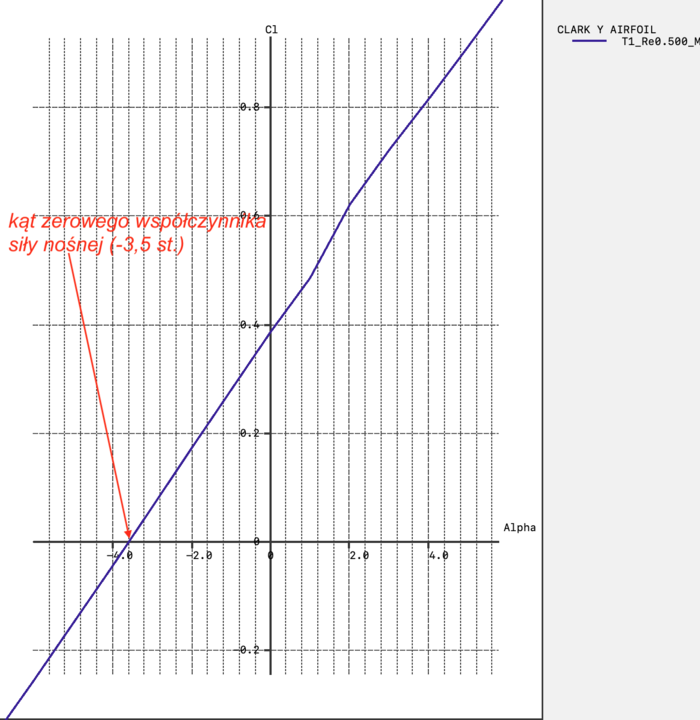
Jest to kąt natarcia dla profilu, dla którego współczynnik siły nośnej wynosi ZERO.

Dla profilu Clark Y jest to -3,5 stopnia.

Jeżeli w locie nurkowym przekroczymy prędkość Vn max, to możemy mieć problem.

Śmigło wytwarza siłę nośną skierowaną w tył - śmigło zaczyna wiatrakować.
Możemy uszkodzić silnik - tłokowy na 99%



Prędkość Vn max można prosto wyliczyć
Z rysunku widać, że maksymalny kąt napływu na profil śmigła w r = 0,75R wynosi β + α (L0) = 15+3,5 = 18,5 [st]
tan(18,5) = 0,3345

Prędkość obwodowa profilu w 0,75R = ω * 0,75R = 755 * 0,75*299 = 169 m/s
Vn max = 169 * tan(18,5) = 169*0,3345 = 56,5 m/s = 203 km/h

Gwarantuję, że model jest w stanie przekroczyć tą prędkość - wystarczy przeanalizować minimalny promień wyrwania z lotu nurkowego.

Czyli - umiemy wyznaczyć maksymalną nieprzekraczalną prędkość naszego modelu


C.2 Geometria śmigła w OpenVSP

Przed pojawieniem się programów CAD, nie było to proste.
Wykonanie rysunków profili śmigła wzdłuż rozpiętości łopaty (promienia śmigła) - to była żmudna praca z wykorzystaniem zasad geometrii wykreślnej oraz obliczeń wg charakterystyk śmigła.

Często śmigło u nasady ma mniejsze cięciwy niż np w 0,5R. Profile mają większą grubość niż wynikałoby to ze standardowej zmiany skali.

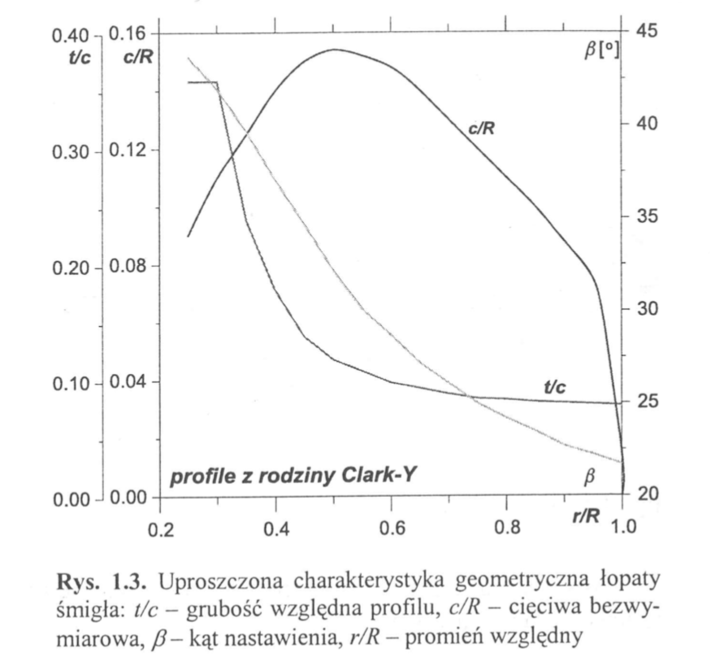
Korzystało się np z takiego wykresu

źródło: Piotr Strzelczyk "Wybrane zagadnienia aerodynamiki śmigieł"

zmiana cięciwy wzdłuż promienia - krzywa: c/R
zmiana kąta β profili łopaty wzdłuż promienia - krzywa: β
zmiana grubości profili wzdłuż wzdłuż promienia - krzywa: t/c

Tutaj nic nie mówiłem o aspektach wytrzymałościowych łopaty śmigła - na 99,99% dla śmigła modelarskiego nie do akrobacji 3D wytrzymałość jest OK jeśli prawidłowo zaprojektowaliśmy śmigło wg tego com przedstawiłem.

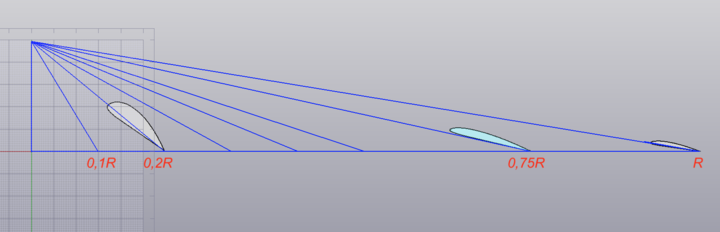
Czyli najpierw trzeba było wykonać taki rysunek poszczególnych przekrojów łopat śmigła.



Później je odpowiedni ustawić w tzw klocku śmigłowym - rysunek powyżej z książki W. Schiera.

Dobrze zaczynamy tworzyć śmigło w OpenVSP.

Zanim ktoś zacznie, dobrze jest obejrzeć kilka tutoriali.
Ja jestem "makowy" - korzystam z wersji: 3.26.1 - uruchamiam skrypt: VSP za pomocą Terminala.

Po otwarciu u mnie są dwa osobne okna:
ekran wyświetlania rysunku - i ekran wyboru elementu konstrukcji samolotu.



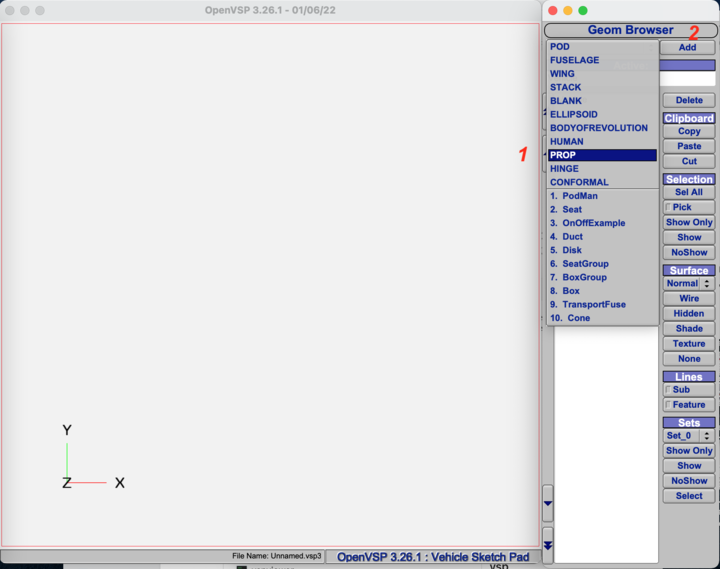
Po rozwinięciu listy wyboru elementów:
1. zaznaczamy: PROP
2. Klikamy przycisk; Add


Domyślnie na ekranie mamy śmigło trójopatowe.


Zmieniamy sobie widok w zakładce: View, w menu głównym programu (górny pasek)

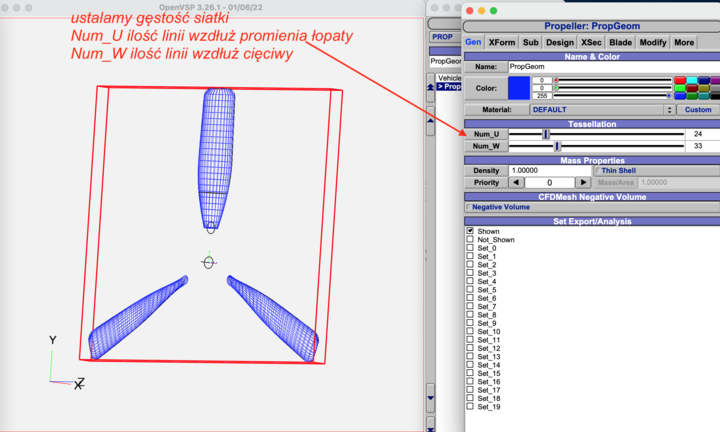
Teraz musimy zadbać o jakość profili poszczególnych przekrojów - do tego używamy ekranu: Propeller:PropGeom - zakładka: Gen (jak powyżej)
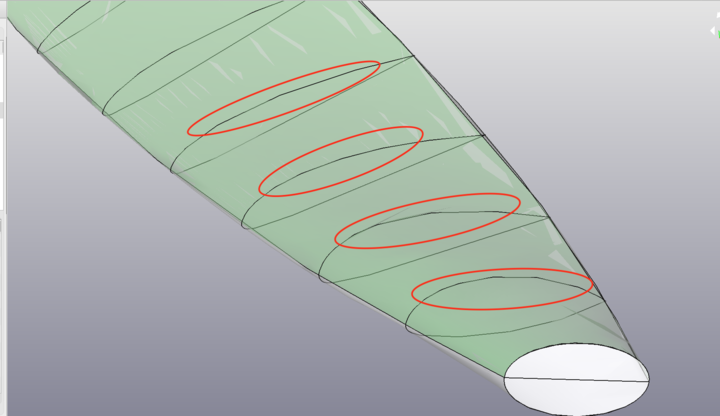
Im więcej tym lepiej dla Num_W (ilość linii wzdłuż cięciwy)
Jeśli będzie za mało - będzie tak po eksporcie do CAD


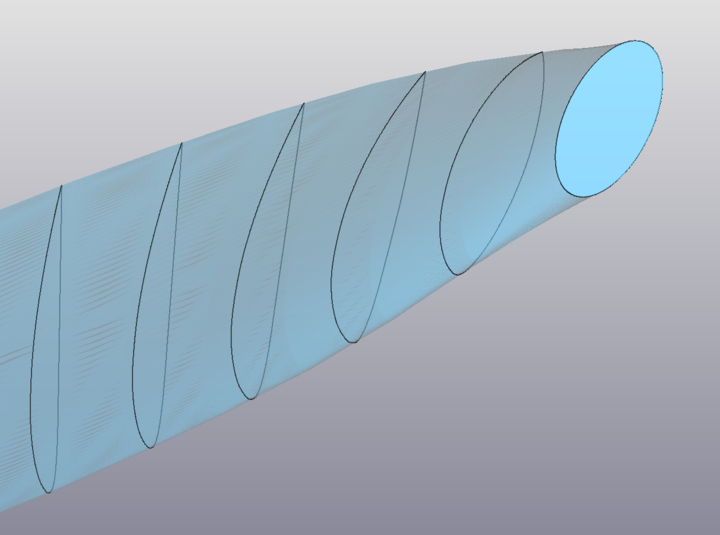
A ma być tak:



C.d w nowym poście ze względu na ograniczenia ilości załączników (1)

_________________
Dobrze jest zostawić po sobie nie tylko smród.

Hmm - takie mi się pojawiło:




C.2 Geometria śmigła w OpenVSP - c.d.

Przechodzimy do zakładki: Design w menu: Propeller:PropGeom


Najpierw decydujemy się w jakich jednostkach będziemy chcieli mieć wymiary liniowe.
Średnica naszego śmigła = 598 mm - proponuję pozostać przy mm.
Używamy kropki dla wartości w ułamkach dziesiętnych - NIE PRZECINKA.

1. W okienku obok suwaka dla Diameter: wpisujemy wymiar średnicy naszego śmigła
2. Num Blades - ilość łopat, zmieniamy 3 na 2;
3. Beta 3/4 - zmieniamy domyślne 20 na 15;
4. ustalamy przekrój nasady łopaty: r_0, domyślnie jest 0.2, może być dowolna wartość. Np. jeśli chcemy zaprojektować tutaj całe śmigło łącznie z piastą, to postępujemy następująco:
4.1. ustalamy średnicę otworu w piaście (średnica wału silnika, lub adaptora). powiedzmy, że ma 10 mm, r_0 ustawiamy trochę powyżej, np. w okolicach 6 mm. Np. r_0 = 0,02R = 0,02*299 = 5,98 mm.
4.2. dla takiej wartości najlepiej wybrać przekrój kołowy.

Teraz przechodzimy do zakładki: XSec i dalej obrabiamy sekcję r_0 łopaty



1. Jeśli w zakładce Design ustaliliśmy r_0 = 0,02, to w tej zakładce musi być tak samo
2. z listy wybieramy kształt przekroju - CIRCLE (okrąg)
3 Jeśli klikniemy w przycisk: Show, pojawi nam się okno: XSec View.

Ja będę kontynuował rysowanie śmigła od r_0 = 0,1R aż do 1R


Ustaliłem 8 sekcji:
r_0 = 0.1R
r_1 = 0.25R
r_2 = 0.35R
r_3 = 0.5R
r_4 = 0.75R
r_5 = 0.875R
r_6 = 0.975R
r_7 = R

Aby dodać koleją sekcję po r_0 - klikamy przycisk: Insert i ustalamy wymiar od osi; sekcja r_1 = 0.25R


Po kliknięciu w listę przekrojów: Choose type, możemy wybrać przekrój dla tej sekcji.
Dla przekroju w r = 0.1R zalecam przekrój eliptyczny, jeśli chcemy bardzo profil lotniczy - wybieramy jak wyżej: AF FILE, lub któryś z listy:
Dla nowoczesnych śmigieł stosuje się profile: 16_SERIES. Nie zalecam do modelarskich.


Do modelarskich zalecam Clark Y lub RAF 6


Dobieranie profili (kształtu) przekrojów poszczególnych sekcji


Przyjmujemy profil do naszego śmigła - Clark Y.
Musimy zatem wczytać plik z rozszerzeniem dat dla tego profilu.
Można pobrać np. z tej strony: http://airfoiltools.com/airfoil/details ... =clarky-il

Zakładamy, że profile lotnicze będą dopiero od sekcji r_1.

Wybraliśmy opcję: AF_FILE, klikamy w przycisk: Read File im poszukujemy w naszym komputerze kilku dat dla profilu Clark Y. Po wybraniu, klikamy w przycisk: Accept.


Program OpenVSP tworzy elemnty funkcji Loft naprawdę bardzo dobrze - tu widać profile przejściowe pomiędzy elipsą w sekcji r_1 = 0.1R a profilem Clark Y w sekcji r_2 = 0.35R


Suwaki dla: Chord i T/C są nieaktywne dla elementu śmigła.
Ustalamy to w inny sposób.

Przechodząc do poszczególnych sekcji możemy podejrzeć profile, klikając w przycisk: Show
Dla r = 0.25R


Dla r = 0,75R


Dla końcówki łopaty: r = R


To, co kiedyś było mozolnym kreśleniem na papierze milimetrowym przy pomocy krzywików, teraz uzyskujemy kilkoma kliknięciami myszy w jakimś tam programie.
W obecnym czasie nie wszyscy wiedzą, co to krzywiki, lub krzywki.

Może Silidworks, i Catia robią też tak dobrze, ale ja jako hobbysta korzystam jedynie a wolnego oprogramowania.
Nie sądzę aby ktoś, kto na codzień w pracy nie używa Catii, kupił sobie pełną licencję dla zastosowań hobbystycznych. Dlatego nie mam litości dal takich ludzi popisujących się projektami np. Silidworks lub Catii na Forach dla hobbystów.
Już Airbus symulował wytrzymałość zmęczeniową napraw struktury typu doubler w Catii.
Efekt jest jaki jet, np dla A320 i innych.

Zakładka: Blade



Tu zajmiemy się tylko kilkoma opcjami menu tej zakładki:
1. Chord - cięciwa;
2. Twist - skręcenie, rozkład kąta beta poszczególnych przekrojów łopaty;
3. Thick - grubość profilu, dla śmigieł modelarskich proponuję zostawić "AS IS" (jak jest), nie mieszać aby nie pogorszyć wytrzymałości łopaty śmigła.
4. Cli - rozkład współczynnika siły nożnej wzdłuż promienia łopaty.

Pozostałe - dla śmigieł modelarskich o stołym skoku nie są za bardzo przydatne.

Teraz musimy wrócić do wytycznych, które przyjęliśmy dla projektowanego śmigła typ: M56
c/D = 1/15, ale może być w zakresie 1/12 do 1/15, czyli w zakresie od 0,083 do 0,066
Tutaj mamy c/R, czyli musimy pomnożyć poprzednie wartości przez 2.

Czyli c/R ma być w zakresie 0,17 do 0,13

Wybierając opcję Chord - projektujemy kształt łopaty wzdłuż promienia.
Możemy wybrać bardziej eliptyczny, lub bardziej prostokątny.
Modelach makiet - kształt ten był bardziej eliptyczny.


Wykres, który widzimy na powyższym rysunku to krzywa c/R wzdłuż promienia łopaty.
Jak widać domyślnie program ma bardziej prostokątny kształt łopaty i dość szeroki.

Najprościej - łapiemy za punkty na wykresie i tworzymy naszą krzywą, aby wartości były w granicach 0.15 +- 0,02
Można się pobawić is sprawdzić jak się zmienia kształt łopaty po zmianie położenia jakiegoś punktu.

_________________
Dobrze jest zostawić po sobie nie tylko smród.

C.2 Geometria śmigła w OpenVSP - c.d.

Twist
Generalnie mamy 3 punkty krzywej
ustalamy kąty beta dla
r_0 = 0.1R
r_1 = 0.75R
r_2 = R



Do tego będzie nam potrzebny taki rysunek. Nie musi być z profilami, ale musimy wyznaczyć wartości tych trzech kątów.


kąt β w r_1 = 0.75R ustaliliśmy na 15 stopni
kąt β w r_2 = R tutaj można przyjąć niewielką wartość ponad wartość wynikającą ze skoku geometrycznego - przyjąłem 10 stopni.



kąt β w r_0 = 0.1R - tutaj zdecydowaliśmy na przekrój eliptyczny - nie ma sensu dawać jakiegoś kąta natarcia dla elipsy, przyjmujemy kat z rysunku 58.7 stopnia


Tak naprawdę, to już ostatni element projektu prostego śmigla modelarskiego.
Wspominałem, że opcją Thick - grubość w przypadku śmigła modelarskiego nie do 3D można się nie zajmować.

Możemy sprawdzić rozkład współczynnika siły nośnej wzdłuż promienia łopaty wybierając w zakładce: Blade opcję CLi


Możecie się pobawić ta krzywą i pozmieniać jej kształt - nic to nie zmieni w kształcie śmigła.
Jest to krzywa wynikowa w tej wersji OpenVSP.


Pozostaje nam eksport pliku do CAD i finalna obróbka np. na frezarkę CNC lub na drukarkę 3D.

_________________
Dobrze jest zostawić po sobie nie tylko smród.

D. Eksport geometrii śmigła z OpenVSP do CAD

Zapomniałem o tym napisać wcześniej, gdyby się okazało, że na ekranie wyświetlania nic nie ma oprócz trzech osi. Wchodzimy w zakładkę View i wybieramy opcję np. Fit On Screen


Eksport do *.stl
Najprościej:
1. Eksportowany obiekt musimy mieć w czerwonych ramkach, możemy wybrać klika obiektów do eksportu;
2. Klikamy: File > Export..


3. Wybieramy: Stereolith(.stl)
UWAGA z tego menu nie robimy exportu do *.stp lub *.igs



4. STL Options
4.1 - zostawiając podświetlony tylko ten kwadracik - OpenVSP wyeksportuje każdą łopatę jako osobny element stl
4.2 - zostawiając podświetlony tylko ten kwadracik - OpenVSP wyeksportuje obie łopaty element stl


Przykład wyniku eksportu wg opcji 4.1 i importu do FreeCAD


Po tej operacji zmieni nam się mesh - jeśli mamy tak jak poniżej (dwa kolory) wybrano opcję eksportu 4.1. Wybierając opcję 4.2. mesh jest tylko jednego koloru (zwykle czerwony)


Eksport do: *.stp, lub *.igs, lub innych formatów

Eksport do tych formatów wykonujemy przez zakładkę: Analysis i wybieramy Trimmed Surfaces
Ale, jedno ale linie siatki muszą być gęste.





Tak naprawdę teraz pozostaje dalsza obróbka w jakimś programie CAD. Tutaj nie będę się ośmieszał. J raczkuję we FreeCAD.
Piastę można dorobić różnymi metodami.

Gotowy rysunek śmigła.
Śmigło można wykonać na różne sposoby.
Z drewna
- metodą dawną,
- na frezarce CNC
Wydrukować 3D

_________________
Dobrze jest zostawić po sobie nie tylko smród.

E. Dodatki i uzupełnienia.

Jeśli potrzebujemy zaprojektować śmigło kręcące się w lewo


Inna aplikacja do obliczania śmigieł modelarskich: BEARCONTROL - działa pod matlabem, nie próbowałem. Opis w tym artykule.



Załączam kalkulator - dwa pliki, jeden z przykładem drugi pusty.
Gdyby ktoś chciał odblokowany - przez PW
Gdyby ktoś zauważył jakiś błąd (ale nie ortograficzny) - pisać: tu lub na PW.

Pierwsza zakładka: silnik, obliczenia (dobór) mocy silnika do modelu z uwzględniam sprawności silnika i śmigła (już pisałem, nie wierzę eCalc prop) - opisane trochę tu: https://pfmrc.eu/topic/93031-obliczenie ... bez-ecalc/

Druga zakładka: śmigło obliczanie, to arkusz obliczeń do projektu śmigła w OpenVSP
Trochę teorii śmigieł jest tu: https://pfmrc.eu/topic/93044-troch%C4%9 ... 9Bmiglach/

Trzecia zakładka: sprawdzenie śmigieł APC, pokazuję jak sprawdzi czy sugerowane przez producenta silnika śmigła są OK.






Sprawdzenie zalecanych przez producenta silnika śmigieł
Najlepiej dokonać wyboru silnika wg zakładki: śmigło, a potem sprawdzić w zakładce: sprawdzenie śmigieł APC
Dlaczego APC tylko, ano dlatego, że tylko wytwórnia APC publikuje dane do tego. Nie wiem skąd twórcy eCalc biorą dane do swego arkusza.

Wszystkie dane śmigieł opublikowane na swojej stronie https://www.apcprop.com/technical-infor ... downloads/

Plik PE0-FILES_WEB-202206.zipx dane geometryczne łącznie z zastosowanym profilem
Plik PERFILES_WEB-202103.zipx - dane osiągów śmigieł.

Pliki maj rozszerzenie *.dat, otwierają się jako txt

Jeśli robiliśmy dobór silnika przy pomocy zakładki silnik - część danych zostanie automatycznie pobrana do tej zakładki.
Wpisujemy sobie zalecane rozmiary śmigieł przez producenta silnika i sprawdzamy.
Jedynie co musimy to wpisać, to zakładaną maksymalną prędkość naszego modelu w locie poziomym.



Już to pisałem:

Dobrze dobrane śmigło do silnika to takie, którego moment oporowy jest równy momentowi użytecznemu silnika.



Sprawdzamy pierwsze śmigło 22 x 10
Maksymalne obroty silnika (i zarazem śmigła) 7215 - wybieramy dane dla RPM 7000


130 km/h to 80,8 mph

Szukamy w kolumnie: Torque dla zakresu prędkości około 80 mph
Widać, że maksymalny moment to 17,141 In-lbs, a nasz silnik wytwarza moment 41,84 In-lbs

To śmigło jest za lekkie do tego silnika i zakładanej prędkości maksymalnej

Sprawdzamy drugie śmigło: 22x12E


Też za lekkie

Sprawdzamy trzecie śmigło: 22x12WE


Śmigło jest OK

Sprawdzamy śmigło 24x12E - 24x12 AXI zaleca do akrobacji 3D


Do zakładanej maksymalnej prędkości jest za ciężkie, model będzie latał znacznie szybciej.



KONIEC

_________________
Dobrze jest zostawić po sobie nie tylko smród.

Jak zwykle - czapki z głów! Świetny materiał/manual!

Pora sprawdzić teorię w praktyce.

Postanowiłem zaprojektować i wykonać własne śmigło o wymiarach 13x6 - tak mi wyszło z wyliczeń dla mojego silnika, który będzie umieszczony w tym modelu.
https://www.rcgroups.com/forums/showthr ... Quickie-Q2

Będę go porównywał ze śmigłem APC 13x6E

Aby cokolwiek porównywać potrzebna jest waga do pomiaru ciągu. Tu też zaprojektowałem i wykonałem swój tester ciągu - wzorowany na rozwiązaniu komercyjnym.

Do testów EDFów:


Tutaj testowałem ciąg EDF do napędu Hortena. (wnioski opiszę w temacie o Hortenie)

I do testów śmigieł - zdjęcie poniżej.

Wracając do śmigła - zaprojektowane w OpenVSP wg tego, co opisałem wcześniej w poradniku.

Śmigło wydrukowane na zwykłej drukarce 3D


Obrobione we FreeCAD
Najpierw drukowałem w całości - ale wychodziło podle.
Zrobione finalnie z czterech elementów: dwie łopaty oraz dwie bazy ustalające - sklejone za pomocą CA.


Wyszło tak:


Śmigło powinno być wzmocnione tkaniną szklaną, ale chciałem się przekonać ile wytrzyma takie z drukarki. Druk z Imact PLA

Śmigło wyważone - pora na testy:


Testowałem na dwóch pakietach: 5S i 6S

Śmigło APC - wyniki:
dla pakietu 5S: 2,021 kg


dla pakietu 6S: 2,630 kg



Moje śmigło - wyniki:
dla pakietu 5S: 2,165 kg


dla pakietu 6S: zdjęcie poniżej.


Śmigło nie wytrzymało, siła nośna i bezwładność łopaty zrobiły swoje.



Wydrukowane kolejne śmigło, wzmacniane tkaniną szklaną 25 g/m2


Wrzucę filmik z testów.

Wstępne wnioski:
- program OpenVSP działa prawidłowo jeśli chodzi o generowanie geometrii śmigła, co mnie bardzo cieszy;
- czy warto się trudzić?
1. Do budowy trenerków, modeli sylwetowych - oczywiście nie warto projektować i drukować, czy też strugać z drewna;
2. Do konstrukcji nietypowych, eksperymentalnych, dziwnych makiet - oczywiście warto.

Wybierając metodę wykonania warto pomyśleć o wytrzymałości łopat.

_________________
Dobrze jest zostawić po sobie nie tylko smród.

Odpuściłem na jakiś czas drukowanie śmigła.

Zrobiłem śmigło na frezarce CNC.

Samo frezowanie -czas całkowity ok. 8 godzin.
Najlepiej byłoby użyć frezarki czteroosiowej, ale mam tylko X,Y,Z.
Dało radę. Trzeba dać trochę większe podpory.

Materiał: próg bukowy zakupiony w markecie budowlanym o wymiarach w mm 1000x100x20

Wersja końcowa


Czas na testy.
Testowałem tylko na pakiecie 5S.
Max ciąg 2,24 kg (Aku 5S). Więcej niż APC.

_________________
Dobrze jest zostawić po sobie nie tylko smród.